HIGH END 2024
09.05.2024 - 12.05.2024
Atrium 4.1, E126
M,O,C, München
Lilienthalallee 40
80939 München

Es gibt viel neues! Klangverbesserungen, Sicherheit und Innovation, und das alles in gewohnter WBT und nextgen™ Qualität.
Besuchen Sie uns auf der nächsten Messe:
09.05.2024 - 12.05.2024
Atrium 4.1, E126
M,O,C, München
Lilienthalallee 40
80939 München

Bei dem deutschlandweiten Innovationswettbewerb 2021, veranstaltet von der WirtschaftsWoche*, EnBW und Accenture und unter der Schirmherrschaft des deutschen Bundeswirtschaftsministeriums, wurde WBT für seine PVD- Verfahrensentwicklung,
WBT-PlasmaProtect™ zum Gewinner gewählt.
Durch dieses Verfahren konnten Kontaktqualität und Langzeitstabilität bei Audio-Steckverbindern verbessert werden:
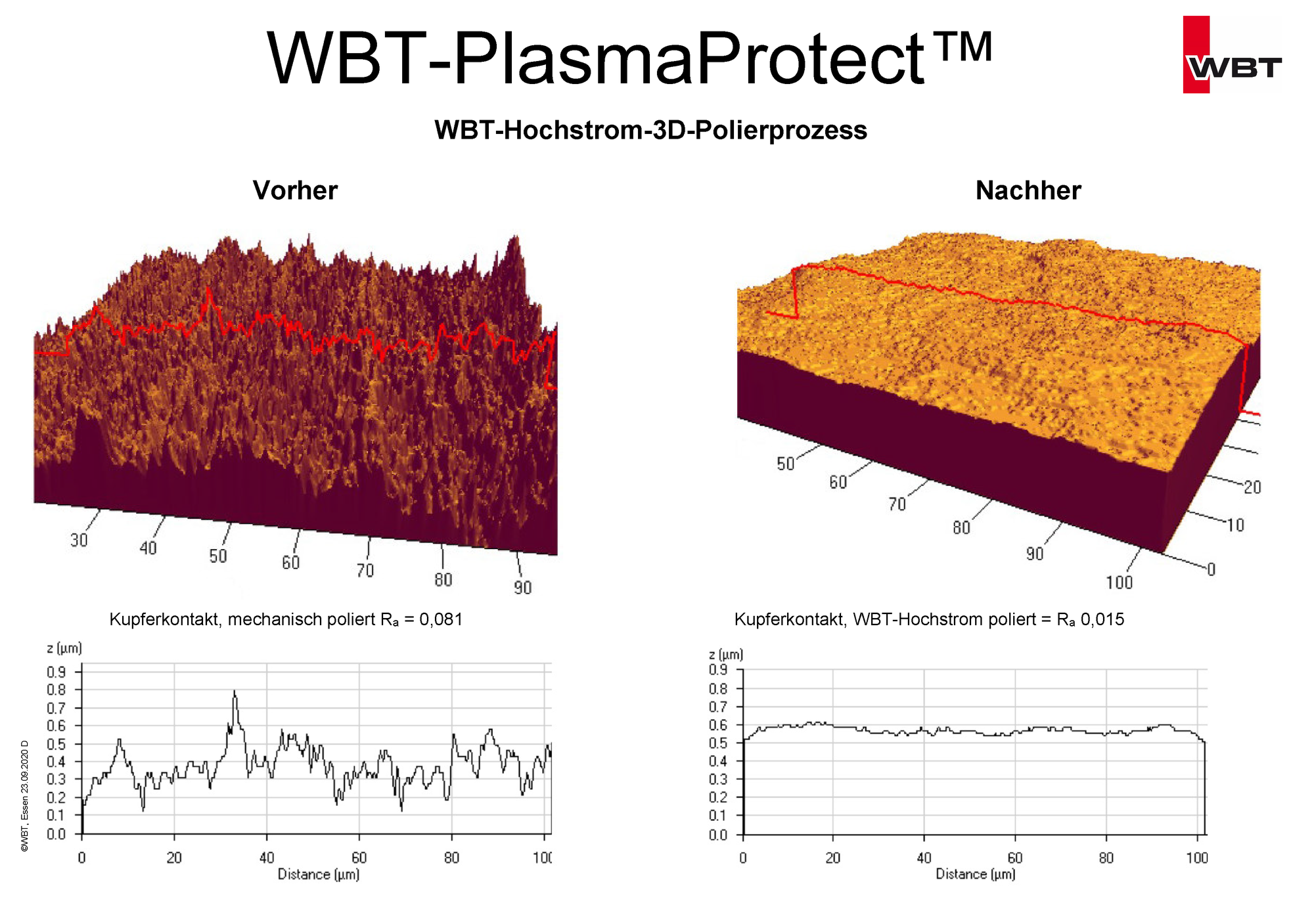
1) Durch die Vorbehandlung mit Hochstrom-Polierung wird die kontaktschädliche
Oberflächenrauhigkeit der Signalleiter ganz erheblich geglättet, so dass die
„Van-der-Waals-Kräfte“ stärker aktiviert werden, damit dann im
PVD-Verfahren direkt beschichtet werden kann, siehe beigefügte Grafik.
2) Die PVD-(Gold)Oberfläche ist fehlerfrei und rein (Hochvakuum), kristallin strukturiert,
dünner und gleichzeitig flexibler mit guter elastischer Verformbarkeit
(Hertzsche Pressung) für eine verbesserte Kontaktqualität.

Außerdem gab es die Auszeichnung für vier weitere Entwicklungsleistungen, die den Sprung von der früheren Galvanik zur modernen PVD-Plasma-Technologie begründen:
1) Die 3D-Beschichtung im PVD-Plasma, verbunden mit der Verbesserung
der Effektivität von ca. 20 auf 80%,
2) die Energieeinsparung von ca. 26%,
3) die Ressourcenschonung (Goldeinsparung) von ca. 35%, und
4) die Umweltentlastung durch den Entfall von toxischen Galvanikbädern.
Durch die Verfahrensentwicklung mit dem direkten Verbund zwischen Hochstrompolierung
und PVD-Plasma Beschichtung konnte die Qualität gesteigert, die Umwelt entlastet
und Ressourcen gespart werden.
Prinzipiell kann diese neue Technik bei allen Steckverbindern, z B. in der Mess- und Regeltechnik, eingesetzt werden. Insbesondere dann, wenn große Breitbandigkeit und hohe Stromtragfähigkeit sowie gleichzeitig eine verbesserte Langzeitstabilität gefragt sind.


Seit vielen Jahren schätzen Liebhaber bester Klangqualität die nextgen™ Steckverbinder von WBT. Mit einem filigranen Signalleiter aus reinem Kupfer oder Feinsilber in Kombination mit modernen Funktionswerkstoffen bietet die nextgen™-Serie alles was das audiophile Herz erfreut. Durch die Masseoptimierung des Signalleiters ist es WBT gelungen Massespeichereffekte und Wirbelströme zu minimieren. Das Klangbild erscheint klarer, mit spürbar mehr Substanz und Räumlichkeit. Das ist WBT aber noch nicht genug. Seit einigen Jahren arbeitet die Ideenschmiede im Hause WBT auf Hochtouren. Nach dem Motto das Beste ist noch lange nicht gut genug hat es WBT sich zur Aufgabe gemacht das nextgen™-Prinzip weiter zu verbessern. Der Weg dahin erschien oftmals steinig und schwer. Die hauseigene Fertigung in Essen musste neu strukturiert werden. Eine PVD-Plasma Fertigung neu entstehen. Schon während der Umbauphase wurden eigene, speziell auf WBT zugeschnittene, Produktionsverfahren entwickelt und eine neue Fertigungsstraße dafür gebaut.

Doch was bedeutet eigentlich eine PVD-Plasma-Fertigung?
Kontakte müssen gegen Korrosion geschützt werden. Dies geschieht bei Steckverbindern weltweit fast ausschließlich mittels Galvanotechnik. WBT jedoch ersetzt als erster Hersteller von Steckverbindern die Galvanik durch die wesentlich präzisere PVD Technik. Die neue Nanotechnologie löst die überholte Galvanotechnik ab. Für diesen Prozess werden die Signalleiter aus reinem Kupfer in einer Hochstrom-Polieranlage von Verunreinigungen befreit und die Oberfläche auf Hochglanz poliert. Dies geschieht gänzlich ohne schädliche chemische Zusätze. Die dabei entstehende Oberfläche ist absolut rein, ohne chemische Einschlüsse, so genannten Fehlstellen. Anschließend wird der Leiter physikalisch Feinvergoldet, im PVD-Verfahren (Physical Vapour Deposition). In diesem wird durch eine im Hochvakuum gezündete Plasmaentladung atomares Gold freigesetzt. Dieses Gold wird im Vakuum regelrecht auf den Kupferleiter geschossen und dadurch atomar angebunden* und somit unlösbar verankert (*van der Waals-Kräfte). Das Resultat ist ein homogener Materialverbund mit einer Oberfläche aus 24-karätigem Gold.

Und warum ausgerechnet Plasma?
Warum Plasma lässt sich schnell erklären. Mit dem nextgen™-Prinzip hat WBT bereits den Anfang gemacht zu einem umweltorientierten Technologiewechsel. Die Umstellung von einer galvanischen Oberflächenbeschichtung hin zum Plasma ist die konsequente Weiterführung dieses Grundgedanken. Im Gegensatz zur umweltschädlichen Galvanotechnik, braucht das Plasmaverfahren keine toxischen Galvanikbäder und ist somit umweltneutral. Ebenso verringert sich der Energiebedarf mit dem neuen Prozess um ca. 25%. Auch wertvolle Edelmetalle können ressourcenschonend eingesetzt werden.

Was macht das mit dem Klang?
Das atomar angebundene Gold sorgt für eine harte und flexible Oberfläche zugleich, die kratz- und abriebfest ist. Wichtiger jedoch ist die Struktur im Material selbst. Durch das PVD-Plasma-Verfahren entsteht eine kristallin geordnete Struktur. Da Elektrizität richtungsabhängig ist ermöglicht diese Struktur einen noch präziseren Signalfluss und dadurch eine unerreichte Signalqualität. Während die nextgen™-Steckverbinder bisher mit mehr Klarheit, Substanz und Räumlichkeit zu einer Klangverbesserung beigetragen haben erscheint mit WBT-PlasmaProtect™ der Klang noch viel definierter. Während man sich immer wünscht das Orchester im eigenen Wohnzimmer spielen zu hören, hat man nun das Gefühl man befinde sich in Mitten des Orchesters. Schließt man die Augen so glaubt man in den Streichern zu stehen und dann wieder inmitten der Bläser. Und ganz plötzlich wieder bei der Pauke. Man gewinnt den Eindruck nicht nur Zuhörer zu sein, sondern ein Teil der Musizierenden. Mit WBT-PlasmaProtect™ gelingt WBT ein Qualitätssprung bei Audio-Steckverbindern.

Der breiten Öffentlichkeit ist vor allem die Markenpiraterie im Bereich der Luxusgüter bekannt. Aber auch die HiFi-Branche ist stark betroffen.
Markenpiraterie ist ein ernstes Problem für die Hersteller und Verbraucher von Qualitäts-Markenprodukten.
In den letzten Jahren hat die Verbreitung von gefälschten Produkten so enorm zugenommen, dass die weltweite Wirtschaft betroffen ist. Verbraucher leiden unter gefälschten Produkten, da die Fälschungen in der Regel nicht als solche erkennbar sind, aber eine schlechtere Leistung und Haltbarkeit haben. Im schlimmsten Fall können sie weitere Hardware stark beschädigen.
Dies wirkt sich wiederum negativ auf die Hersteller aus, deren Markenimage ernsthaft beschädigt werden kann.
WBT ist sich der Tatsache bewusst, dass gefälschte WBT-Steckverbinder nicht nur in Europa, sondern auch weltweit im Umlauf sind. Wir sind bestrebt diese illegalen Produkte vom Markt zu entfernen und werden alle Hersteller und Händler, die die Integrität der Marke WBT mit Ihren Aktivitäten untergraben, mit voller Härte strafrechtlich verfolgen.
Beachten Sie:
Wenn der Preis zu gut ist, um wahr zu sein, kaufen Sie wahrscheinlich keine Original-Produkte von WBT! Wenn Sie sich über die Herkunft Ihrer Steckverbinder nicht sicher sind, wenden Sie sich an Ihren WBT-Händler oder an WBT direkt. Wir helfen Ihnen gerne Ihren Kauf zu überprüfen.
WBT-Industrie GmbH
Telefon: 02054 – 87552 -50
sales@wbt.de